前回記事
この記事では以前概要をまとめた、【要約】行動経済学ってそういうことだったのか!【紹介】の内容をさらに深堀りながら復習していきます。
著書で紹介されている“プロスペクト理論”や“ナッジ”などの専門用語を中心に定期的に1、2テーマずつまとめようと思います。
今回のテーマは“確率加重関数”です。

前回記事のテーマであるプロスペクト理論では、損する悲しみは得する喜びよりも大きいということ、人は損を回避する傾向にあることをまとめました。
また100万円のボーナスをもらったとしても、元々200万円貰える予定だったのか、元々50万円貰える予定だったのかによって満足度が大きく変わること、そのことから人の満足度は水準ではなく変化であることも分かりました。
カーネマン氏らは、「物事の変化によって価値観が変わるのなら、確率についても変化によって感じ方が変わるのでないか」と考えました。
それを体系的にまとめたものが今回紹介する“確率加重関数”です。
確率加重関数

確率加重関数とは、確率の感じ方に歪みがあることを表す関数のことです。
人間が感じている確率とも言い換えられます。
ややこしいので“高い確率は低く、低い確率は高く感じられる”ということだけ知ってくれれば十分です。
さてここでお馴染みの質問タイムです。
【質問①】
ある確率52%と54%があります。
このふたつの差は大きいと感じますか?
たった2%の差ではありますが、大きいと感じるか小さいと感じるかは人それぞれです。
では次の質問。
【質問②】
ある確率98%と100%があります。
このふたつの差は大きいと感じますか?
多くの人は同じ2%の差でも大きな違いを感じているはずです。
カーネマン氏らの研究でも100%からほんの少しでも確率が下がると、感じる評価はそれよりも下がることが明らかになっています。
また人間には高い確率の中でも100%を高く評価する傾向があり、これを“確実性効果”と言います。
それほど100%と98%には大きな差があるのですね。
当選確率の低い宝くじの心理
先ほど100%から少しでも下がると評価はガクッと下がると言いました。
ではなぜ当選確率の極めて低い宝くじの高額当選に心をときめかせる人がいるのでしょうか。
その謎を解く鍵も確率加重関数にあります。
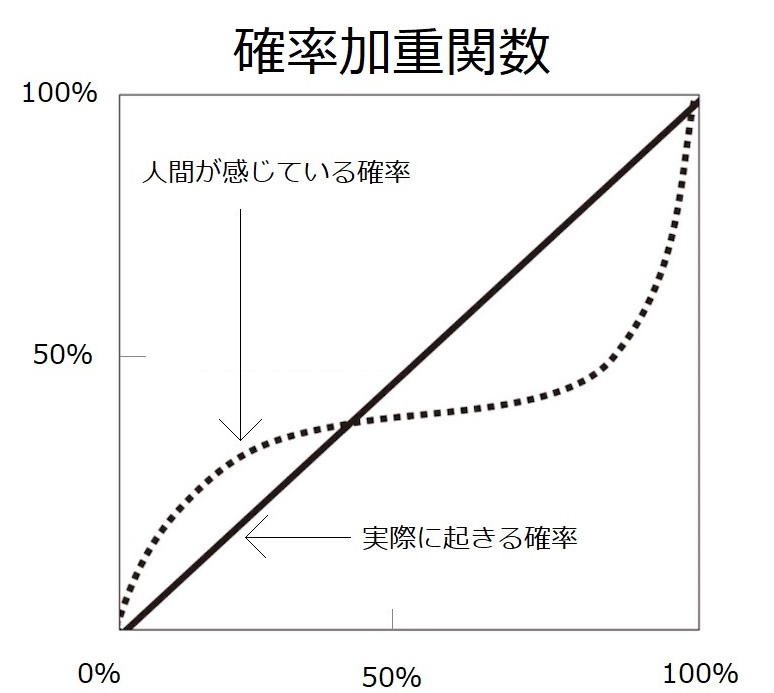
この表はカーネマン氏らの研究からまとめた確率加重関数のグラフです。
グラフを見ると、実際の確率が40%だと感じる確率も40%前後になります。
実際の確率が80%だと感じる確率は60%くらい。
実際の確率が10%だと感じる確率は20%くらい。
40%の水準から離れるにつれて、確率の認識に大きな歪みが表れることを表しています。
この研究で分かったもう一つのポイントは、“非常に低い確率でも、高く評価してしまう”という点です。
非常に低い確率とは、自分には一生起こりえない確率だとしても有効です。
2021年の年末ジャンボ宝くじの1等である7億円が当たる確率は0.00000005%(2,000万分の1)。
この確率は雷に打たれる確率0.000001(100万分の1)よりも低いです。
しかし「0%ではない!」と思うだけで、なんだか当たるかもしれないという感情を引き起こすのです。
この小さい確率を高く評価することを“可能性効果”とも言います。
まとめ
・確率加重関数=実際の確率と人が感じる確率の歪み
・100%から少しでも下がると評価低
・きわめて少ない確率でも0%でなければ評価高
・高額宝くじ当選への期待は確率の歪みが原因
以上、確率加重関数についてのまとめでした!
漫画の主人公たちが土壇場で使う「可能性がゼロじゃないなら俺たちはあきらめない!」的なセリフは、可能性効果の表れだったのですね。
現実に生きる私たちは、目の前の確率の歪みに惑わされないように、冷静に対処する方法を考えられると良いかもしれませんね!
次回記事




















コメント